Capítulo 3: Operações com Números Binários no Microprocessador
3.1 Introdução
Em um computador, as operações aritméticas são realizadas em 8 bits, 16 bits, 32 bits ou 64 bits. Um número como 3 em binário é 11. Se a operação for feita em 8 bits, será considerado 00000011; precedendo-o com 0 zeros.
Para um número binário como 10000101, o bit mais significativo é o bit mais à esquerda. É 1 neste caso. O bit menos significativo é o bit extremo à direita, que ainda é 1, para o número. O bit mais significativo é abreviado como MSB. O bit menos significativo é abreviado como LSB.
O dígito BInário é abreviado como BIT e é simplesmente escrito como bit. No número 10010011, cada um ou zero é um bit. Um grupo de quatro bits é chamado de nibble. Um grupo de oito bits é chamado de byte. Um byte consiste em dois nibbles. O nibble inferior é o nibble para o LSB e o nibble mais alto é o nibble para o MSB.
Um grupo de 8 bits, 16 bits, 32 bits ou 64 bits é chamado de palavra, desde que esse grupo transmita informações além de apenas indicar um número. O grupo é chamado de palavra, por exemplo, se for uma instrução de baixo nível no computador. Há também uma palavra de 24 bits, mas que não é comumente usada hoje.
Endianness refere-se à ordem em que os bytes formam uma palavra. Considere a palavra de 24 bits – 100100001111010100100010. Esta palavra consiste em três bytes que são:
10010000 11110101 00100010
O byte mais significativo é o byte mais à esquerda. Quando o byte na extrema esquerda é o byte mais significativo e o byte na extrema direita é o byte menos significativo, isso é chamado de representação Big Endian da palavra. A representação do Little Endian é o oposto.
A memória do computador é uma série de células e cada célula contém um byte. A primeira célula da memória do computador é para o byte 0, a segunda é para o byte 1, a terceira é para o byte 2 e assim por diante. Com big endianness e para a palavra anterior, o byte mais significativo é armazenado na célula do byte 0, o byte do meio é armazenado na célula do byte 1 e o byte menos significativo é armazenado na célula do byte 2. Isso significa que há bytes mais significativos na célula de memória inferior.
A palavra anterior de 24 bits pode ser escrita na ordem inversa dos bytes da seguinte forma:
00100010 11110101 10010000
Agora, o byte menos significativo está na extrema esquerda e o byte mais significativo está na extrema direita. Quando o byte na extrema esquerda é o byte menos significativo e o byte na extrema direita é o byte mais significativo, é a representação Little Endian da palavra. Com pouco endianness e para a palavra anterior, o byte menos significativo é armazenado na célula do byte 0, o byte do meio é armazenado na célula do byte 1 e o byte mais significativo é armazenado na célula do byte 2. Isso significa que há um byte menos significativo na célula de memória inferior.
Endianness não é usado para bits em um byte. Também não é usado para petiscos em um byte. É usado apenas para ordem de bytes.
A linha numérica
Um número sem sinal é um número positivo. Números positivos são números de zero para cima. Também existem números negativos. Números positivos e negativos podem ser apresentados em uma reta numérica. A seguinte reta numérica mostra os números inteiros positivos e negativos (inteiros) próximos de zero:
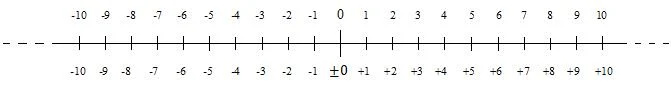
Os números negativos diminuem de zero para baixo (para a esquerda). Em muitas situações, zero é considerado positivo. No entanto, é considerado negativo em algumas situações. É por isso que há um sinal de mais e de menos antes de zero, na numeração inferior, no diagrama. Quando um número é positivo, o seu sinal pode ser omitido; este é o caso da numeração superior no diagrama. O sinal de menos antes de um número negativo nunca é omitido.
3.2 Adição de Números Binários
Além disso:
A + B = S
A é chamado de augundo, B é chamado de adendo e S é chamado de soma.
Considere a seguinte adição de dois números positivos na base dois:

Na base dois, os únicos dígitos possíveis são 0 e 1. A adição na base 2 é semelhante à adição na base dez, mas dois na base dois é um zero (10). Quando a soma de dois bits em uma coluna é 10, 0 é escrito e 1 é transportado para a coluna imediatamente à esquerda; a ser adicionado à soma dos dois bits ali. Quando a soma total é três, significa 11 na base dois. O 1 da direita em 11 é escrito e o 1 da esquerda é transportado para ser adicionado à soma dos bits imediatos da coluna esquerda. Em ambos os casos, o 1 transportado para a esquerda é chamado de carry.
Lendo a tabela de adição anterior da direita, na segunda coluna (da direita), há um carry que resulta de 1+1 = 10. Na terceira coluna, há um carry que resulta de 1+1+ carry de 1 = 11. Na quarta coluna, há um transporte que resulta de 0+1+ transporte de 1 = 10. Na quinta coluna, não há transporte porque a soma é 0+0+ transporte de 1 = 1. O o resto das colunas não envolve transporte.
A contagem de colunas começa na extremidade direita. Com a adição de 16 bits, pode haver um transporte da oitava coluna para a nona coluna (movendo-se para a esquerda). A tabela a seguir ilustra isso:

As operações aritméticas e lógicas ocorrem no microprocessador da placa-mãe do computador.
Para um computador Word de 8 bits, o transporte não pode ir do oitavo para o nono bit automaticamente pelo hardware. Portanto, para adicionar dois grupos de 16 bits em tal computador, a adição deve ser feita duas vezes em pares de oito a oito bits. O carry é movido e efetuado pelo software (programação).
Para adicionar dois números, os números podem ser convertidos primeiro para a forma de complemento de dois (veja abaixo) antes de adicionar.
3.3 Complemento de dois e sua subtração de números binários
Na placa-mãe do computador está a memória e está o microprocessador e outros circuitos. A memória é uma série de células de oito bits. Para um byte, cada bit vai para uma célula. O microprocessador possui alguns locais do tipo memória. Esses locais do tipo memória são chamados de registradores. Assim, no computador, grupos de bytes podem ser armazenados temporariamente na memória ou nos registros do microprocessador.
Em qualquer um desses armazenamentos, cada célula pode receber 1 ou 0 e nada mais. Na vida, existem números positivos e negativos. Um número positivo começa com um sinal de mais (+) e um número negativo começa com um sinal negativo (-). Quando o sinal é omitido, o número é considerado um número positivo.
Para resolver este problema de indicação do sinal de um número no computador, os números inteiros são armazenados em intervalos. Números inteiros são inteiros. Se oito bits forem usados para armazenar o intervalo de números possíveis, o bit mais à esquerda será usado como bit de sinal. Se o número começar com 0, o número é um número positivo. Se começar com 1, o número é negativo. Se dezesseis bits forem usados para armazenar o intervalo de números possíveis, o bit mais à esquerda será usado como bit de sinal. Se o número começar com 0, t o número é um número positivo. Se começar com 1, o número é negativo. Os números neste formato são chamados de números assinados.
Na prática, pode haver números assinados para 8 bits, 16 bits, 32 bits e 64 bits. Quanto maior o número de bits usados, maior será o intervalo de números possíveis que podem ser armazenados.
Inteiros em complemento de dois
Com complemento de dois, os números positivos são os números normais de contagem, exceto que o dígito mais à esquerda é 0. Para obter o número negativo correspondente para qualquer número positivo, inverta cada bit do número e adicione 1 ao resultado. O inverso ou complemento de 0 é 1. O inverso ou complemento de 1 é 0. As tabelas a seguir mostram alguns números em complemento de dois em seus intervalos:
| Tabela 3.31 Inteiros de complemento de dois em dois bits |
|
|---|---|
| Binário | Decimal |
| 01 | +1 |
| 00 | +0 |
| onze | -1 |
| 10 | -2 |
Os números binários positivos são 00 e 01 (ou seja, zero e um). No bit mais à esquerda, zero mostra que são números positivos. 00 está um pouco no meio do intervalo. Para obter -1, o inverso do número 01 é 10. Adicionar 1 a isso (na extrema direita) dá 11.
Como são usados dois bits, resta apenas um bit para representar os números no intervalo que consiste nos números +1, +0 e -1 correspondentes a 01, 00 e 11. O primeiro bit indica o sinal. Acontece que 10 para +2 não está entre esses três números binários. 10 começa com 1, o que significa que deve ser um número negativo em complemento de dois. Portanto, 10 está incluído no intervalo, o que significa -2.
Com dois bits em complemento de dois, o número de todos os inteiros (positivos e negativos) que podem ser representados é 2 2 = 4 e não 2 2 -1 = 3. A nuance resulta da inclusão do último número negativo que é o negativo de 2 número com – 1. Neste caso, -2 2-1 = -2 1 = -2. Não há +2 no intervalo de números em complemento de dois em 2 bits.
| Tabela 3.32 Inteiros de complemento de dois em quatro bits |
|
|---|---|
| Binário | Decimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Os números binários positivos vão de 0000 a 0111 (ou seja, de zero a sete). No bit mais à esquerda, zero mostra que são números positivos. 0000 está um pouco no meio do intervalo. Para obter -1, o inverso do número 0001 é 1110. Adicionar 1 a isso (na extrema direita) dá 1111. Para obter -2, o inverso de 0010 é 1101. Adicionar 1 a isso ( da extrema direita) dá 1110. Os outros números binários negativos, como -3 a -7, são determinados de forma semelhante.
Como são usados quatro bits, restam três bits para representar os números no intervalo que são +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 e -7 correspondentes a 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 e 1001.
O -8 que corresponde a 1000 deve ser endereçado separadamente. O primeiro bit para todos esses números indica o sinal 0 para números positivos e 1 para números negativos. Acontece que 1000 não está entre esses quatorze números binários. 1000 começa com 1, o que significa que deve ser um número negativo, no que diz respeito ao complemento de dois. Portanto, 1000 está incluído no intervalo, o que significa -8.
Com quatro bits em complemento de dois, o número de todos os inteiros (positivos e negativos) que podem ser representados é 2 4 = 16 e não 2 4 – 1 = 15. A nuance resulta da inclusão do último número negativo que é o negativo de 2 númeroLargura – 1. Neste caso, -2 4 -1 = -2 3 = -8. Não há +8 no intervalo de números.
A análise anterior para dois, quatro e bits mais largos em complemento de dois pode ser aplicada a números binários de 8 bits, 16 bits, 32 bits e 64 bits de largura.
O complemento de dois sacrifica o primeiro bit (mais à esquerda) pelo sinal de 0 para número positivo e 1 para número negativo. Para o grupo de bits com largura de “n” bits, existem 2 n total de números positivos mais negativos. Seria 2 n -1, não fosse o último (menor) número negativo da sorte incluído. O maior número positivo é +2 n-1 -1 e o menor número negativo é -2 n-1 -1. Seria -2 n-1 -1, se não fosse pelo sortudo -2 n-1 incluído.
Subtraindo números em complemento de dois
Em subtração:
A – B = D
A é chamado de minuendo, B é chamado de subtraendo e D é chamado de diferença.
Para subtrair um número binário positivo de outro número binário positivo, o minuendo é escrito em complemento de dois e o subtraendo é convertido em seu valor negativo de complemento de dois. Assim, a afirmação matemática torna-se:
A+ – B = D
Em outras palavras, na subtração em complemento de dois, o subtraendo é convertido em um número negativo e depois adicionado ao minuendo.
Exemplo 3.31:
Avalie a seguinte expressão decimal em complemento de dois usando quatro bits:
6 – 4
Solução:
O número binário para 6 é 110. No complemento de dois de 4 bits, é 0110. O número binário para +4 é 100. No complemento de dois de 4 bits, é 0100. 0100 que deve ser convertido em menos 4 em dois. complemente da seguinte forma: O complemento ou inversão de 0100 é 1011. Adicionar 1 a isso da extremidade direita, como fizemos na adição, dá 1100. Portanto, a expressão decimal é:
6 – 4 que se torna:
0110 – 0100 que é
0110 +(– 0100) = 0110 + 1100 feito como na seção de adição anterior como:

Nota: 0110 +(– 0100) é igual a 6 + – 4
Com a subtração do complemento de dois, qualquer transporte, após a última coluna à esquerda, na adição, é descartado. Ao subtrair em decimal, a afirmação matemática é:
6 – 4 = 2
Fazendo a mesma coisa em complemento de dois, a resposta é 0010, que é +2 na contagem binária em complemento de dois. A subtração anterior subtrai um número menor de um número maior. No exemplo a seguir, um número maior é subtraído de um número menor. A Tabela 3.32 pode ser consultada para ver se 0010 é realmente um complemento de dois que equivale a +2.
Exemplo 3.32:
Avalie a seguinte expressão decimal em complemento de dois com quatro bits:
4 – 6
Solução:
O número binário para 4 é 100. No complemento de dois de 4 bits, é 0100. O número binário para +6 é 110. No complemento de dois de 4 bits, é 0110. 0110 deve ser convertido em menos 6 no complemento de dois. da seguinte forma: O complemento ou inversão de 0110 é 1001. Adicionar 1 a isso a partir da extremidade direita, como fizemos na adição anterior, dá 1010. Portanto, a expressão decimal é:
4 - 6 que se torna:
0100 – 0110 que é
0100 +(– 0110) = 0100 + 1010 feito como na seção de adição anterior como:

Nota: 4+ – 6 é igual a 0100 +(– 0110).
Com a subtração do complemento de dois, qualquer transporte, após a última coluna à esquerda, na adição, é descartado. Ao subtrair em decimal, a afirmação matemática é:
4 – 6 = -2
Fazendo a mesma coisa em complemento de dois, a resposta é 1110, que é -2 na contagem binária em complemento de dois. A Tabela 3.32 pode ser consultada para ver se 1110 é realmente um complemento de dois, o que equivale a -2.
3.4 Multiplicação de Números Binários
Na declaração:
A x B = P
A é chamado de multiplicando, B é chamado de multiplicador e P é chamado de produto. A expressão A x B significa adicionar um número de vezes A, B quando A e B são inteiros (números inteiros).
Multiplicação em binário é o mesmo que multiplicação em decimal. Porém, em vez de fazer isso em decimal, é feito em binário. A multiplicação da expressão decimal de 42 x 10 é feita em binário da seguinte forma onde 42 10 = 101010 2 e 10 10 = 1010 2 :
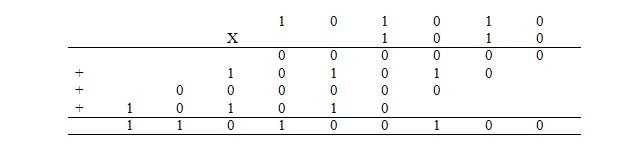
Os 4 números adicionados são denominados produtos parciais. A resposta é o produto. A adição dos produtos parciais é feita da mesma forma explicada anteriormente.
A multiplicação também pode ser vista da seguinte forma: Nesta multiplicação de base dois, se o bit (dígito) no multiplicador for 1, o bit menos significativo de seu produto parcial é o bit menos significativo do multiplicando que é redigitado diretamente abaixo dele; e o resto dos bits do multiplicando são repetidos para a esquerda. Nesta multiplicação de base dois, se o bit (dígito) no multiplicador for 0, seu produto parcial consiste em 0 com o bit menos significativo de 0 diretamente abaixo dele. O número de todos os zeros é o número de bits no multiplicando.
3.5 Divisão de Números Binários
Na declaração:
UMA÷B = Q
A é chamado de Dividendo, B é chamado de Divisor e P é chamado de Quociente. O quociente pode ser acompanhado por um resto. A expressão A ÷ B significa quantas vezes B pode ser adicionado para dar A ou estar próximo dele de modo que o resto seja 0 ou menor que B.
A divisão pode ser feita de várias maneiras. A divisão mostrada aqui é a divisão de restauração.
Restaurando Divisão
Este é o método de divisão longa que é aprendido nas escolas. Se 237 for dividido por 6, a resposta será 39, resto 3. O 237 10 na base 2 é 11101101 2 e 6 10 na base 2 é 110 2 . O 39 10 na base 2 é 100111 2 e 3 10 na base 2 é 11 2 .
Então, 11101101 2 dividido por 110 2 dá 100111 2 restante 11 2 na base dois. Com o método de restauração, os números binários são números comuns e não estão necessariamente em complemento de dois. A seguinte estrutura divide 11101101 2 por 110 2 para dar 100111 2 restante 11 2 :

A subtração é feita normalmente e não usando o complemento de dois. Como esta é a base dois, um empréstimo é dois e não dez. Os dividendos parciais são 10, 101, 1.011, 1.010 e 1.001. 11 é o restante. Como o divisor possui três dígitos, a divisão é feita basicamente em grupos de três dígitos a partir do dividendo determinado. O quociente é o número inteiro (inteiro) e é 100111 para este problema. O resultado do quociente e do restante é o esperado.
3.6 Operações Aritméticas com Software e Hardware
A placa-mãe do computador possui um relógio. Os tiques do relógio são chamados de pulsos. A cada pulso de clock, uma ou mais decisões são tomadas em locais diferentes da placa-mãe; e isso tem a ver com programação (software).
Dentro do microprocessador, existem dois tipos de circuitos chamados: Circuitos Lógicos Combinacionais e Circuitos Lógicos Sequenciais. Existe outro tipo de circuito chamado multiplexador. Adição, multiplicação e divisão podem ocorrer dentro de um intervalo de clock usando a lógica combinacional (circuito). Enquanto a programação (software) compromete a decisão a cada pulso de clock usando circuitos lógicos sequenciais e multiplexadores.
Quando a subtração é feita em complemento de dois, são necessários pelo menos dois pulsos de clock. No primeiro pulso de clock, um multiplexador canaliza o subtraendo para um conjunto de portas NOT (uma porta NOT por dígito). No segundo pulso de clock, a lógica combinacional adiciona 1 à saída das portas NOT e continua a adicionar o subtraendo e o minuendo resultantes. Toda essa adição pode ocorrer dentro de um intervalo de clock.
Adição, multiplicação e divisão ainda podem falhar com a programação usando tabelas verdade. No entanto, isso não é abordado neste curso de carreira online.
3.7 Operações Lógicas no Microprocessador
E, OU, XOR e Inverter
E
A tabela a seguir ilustra o AND bit a bit. Isso significa que para dois números binários diferentes, os bits correspondentes recebem AND com base na tabela AND Truth:
Movendo-se da esquerda para a direita, 1 AND 1 = 1; 0 E 1 = 0; 0 E 0 = 0; 1 E 0 = 0; e assim por diante, de acordo com a Tabela Verdade AND.
OU
A tabela a seguir ilustra o OR bit a bit. Isso significa que para dois números binários diferentes, os bits correspondentes recebem OR com base na tabela OR Truth:

Movendo-se da esquerda para a direita, 1 OR 1 = 1; 0 OU 1 = 1; 0 OU 0 = 0; 1 OU 0 = 1; e assim por diante, de acordo com a Tabela Verdade OR.
LIVRE
A tabela a seguir ilustra o OR exclusivo bit a bit. Isso significa que para dois números binários diferentes, os bits correspondentes são submetidos a XOR com base na tabela XOR Truth:

Movendo-se da esquerda para a direita, 1 XOR 1 = 0; 0 XOU 1 = 1; 0 XOU 0 = 0; 1 XOU 0 = 1; e assim por diante, de acordo com a Tabela Verdade XOR.
Inverter (NÃO)
A tabela a seguir ilustra o NOT bit a bit (invertido). Isso significa que para um número binário, desta vez, cada bit é invertido com base na Tabela Verdade NOT:

Movendo-se da esquerda para a direita, NOT 1 = 0; NÃO 0 = 1; NÃO 0 = 1; NÃO 1 = 0; e assim por diante, de acordo com a tabela NOT Truth.
Mudando para a direita ou para a esquerda
Deslocar para a direita
O seguinte número binário é deslocado 3 posições de bit para a direita, com os zeros inseridos nas posições de bits vagas à esquerda:

A mudança pode ser feita para um, dois, três, quatro, etc.
Deslocar para a esquerda
O seguinte número binário é deslocado 3 posições de bit para a esquerda, com os zeros inseridos nas posições de bits vagas à direita:

A mudança pode ser feita para um, dois, três, quatro, etc.
Girando para a direita ou para a esquerda
Girar é semelhante a mudar. Isso é feito um pouco de cada vez. Ao girar para a direita, os bits que saem da extremidade direita não caem como no deslocamento; eles substituem os bits vagos à esquerda, um por um. Ao girar para a esquerda, os bits que saem da extremidade esquerda não caem como no deslocamento; eles substituem os bits vagos à direita, um por um.
Vire à direita
O seguinte número binário é girado 3 posições de bit para a direita:

A rotação pode ser feita para um, dois, três, quatro, etc.
Rorate à esquerda
O seguinte número binário é girado 3 posições de bit para a esquerda:

A rotação pode ser feita para um, dois, três, quatro, etc.
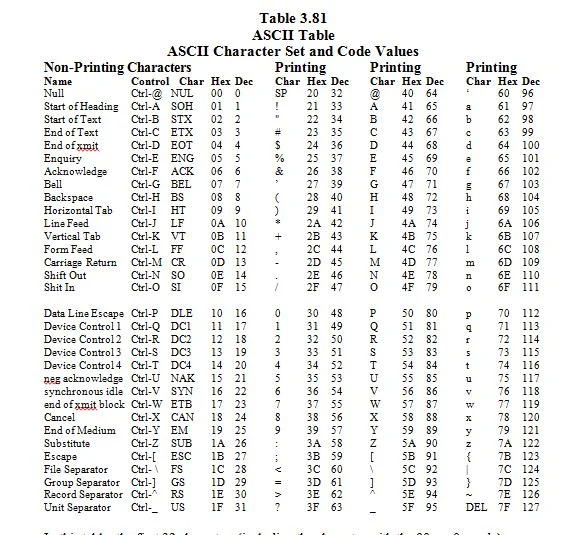
3.8 Conjunto de caracteres ASCII e seus valores de código
ASCII significa “Código Padrão Americano (EUA) para Intercâmbio de Informações”. Imagine um teclado com 96 teclas. Este é um teclado ideal onde as teclas das letras maiúsculas são diferentes das teclas das letras minúsculas. Todas as outras teclas representam um caractere encontrado em um teclado inglês (EUA). Os caracteres e códigos (números correspondentes aos caracteres) estão listados a seguir:
Nesta tabela, os primeiros 32 caracteres (incluindo o caractere com 00 16 = 0 10 código) são caracteres não imprimíveis. Eles são personagens de controle. Eles não são vistos na tela (monitor) onde tudo é igual. Eles só têm efeitos. Vamos discutir mais sobre isso mais tarde.
O restante dos caracteres são caracteres impressos; eles são vistos na tela. Existem 128 caracteres ASCII. 2 7 = 128. 1.111.111 2 = 127 10 . O 7 em 2 7 significa 7 bits.
Agora, 1111111 2 + 1 2 é o mesmo que:
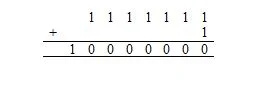
Aqui, 10.000.000 2 = 128 10 . Existem 128 10 caracteres na lista anterior (tabela) de caracteres ASCII. Isso inclui o caractere nulo, cujo código na base dezesseis (hexadecimal) é 00, que equivale a 0 na base dez.
Como há 128 caracteres no total, 128 menos 32 caracteres não imprimíveis resultam em 96 caracteres imprimíveis. Nesta seção, presume-se que existe um teclado ideal com 96 caracteres que podem ser impressos. Neste teclado ideal, as teclas dos caracteres maiúsculos do inglês são diferentes das teclas dos caracteres minúsculos do inglês.
Cada caractere do teclado é representado por um número base dois de 7 bits que não é mostrado na lista. A letra maiúscula de “N”, por exemplo, é representada pelos sete bits 1001110 na base 2. Para converter 1001110 2 para a base 16, preceda-o com 0 e agrupe o resultado em subgrupos de quatro bits da seguinte forma:
| 0100 | 1110 | 2 = | 4 | E | 16
Isso é 01001110 2 = 4E 16 . Para converter 4E 16 para a base dez, faça o seguinte:
4 x (16) 1 + Ex (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
À direita de “N” na lista (tabela) está o número hexadecimal de 4E e o número decimal de 78.
Como outro exemplo, o caractere “[“ é representado pelos sete bits 1011011 na base 2. Para converter 1011011 2 para a base 16, preceda-o com 0 e agrupe o resultado em subgrupos de quatro bits da seguinte forma:
| 0101 | 1011 | 2 = | 5 | B | 16
Isso é 01011011 2 = 5B 16 . Para converter 5B16 em base dez, faça o seguinte:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
À direita de “[“ na lista (tabela) está o número hexadecimal de 5B e o número decimal de 91.
Ainda como outro exemplo, o caractere do número decimal “5” é representado pelos sete bits 0110101 na base 2, e não 0000101 na base 2. Para converter 0110101 2 para a base 16, preceda-o com 0 e agrupe o resultado em subgrupos de quatro bits da seguinte forma:
| 0011 | 0101 | 2 = | 5 | B | 16
Isso é 00110101 2 = 35 16 . Para converter 3516 em base dez, faça o seguinte:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
À direita de “5” na lista (tabela) está o número hexadecimal 35 e o número decimal 53.
Como o computador funciona em bytes, quando uma tecla do teclado ideal é pressionada, oito bits são enviados ao microprocessador (placa-mãe). O teclado ideal é um periférico separado da unidade de sistema (base) do computador. Possui um circuito eletrônico (IC) que cria os sete bits e o precede de um zero antes de enviá-lo através de seu cabo para a placa-mãe da unidade de sistema. Da porta de entrada (circuito de entrada) da placa-mãe, ele vai para o microprocessador que também fica na placa-mãe. Do microprocessador vai para a memória que também vem instalada na placa-mãe.
Assim, quando a tecla “N” do teclado ideal é pressionada, oito bits 01001110 são levados para o microprocessador. Do microprocessador eles são levados para a memória onde permanecem em um local de memória como um byte. O programador de computador deve ter em mente que os oito bits de 01001110 2 é o mesmo que 4E 16 que é o mesmo que 78 10 .
Quando a tecla “[“do teclado ideal é pressionada, oito bits 01011011 são levados para o microprocessador. Do microprocessador eles são levados para a memória onde permanecem em um local de memória como um byte. O programador de computador deve ter em mente que os oito bits de 01011011 2 é o mesmo que 5B 16 que é o mesmo que 91 10 .
Quando a tecla “5” do teclado ideal é pressionada, como caractere e não como número decimal, oito bits 00110101 são levados ao microprocessador. Do microprocessador eles são levados para a memória onde permanecem em um local de memória como um byte. O programador de computador deve ter em mente que os oito bits de 00110101 2 é igual a 35 16 que é o mesmo que 5310 10 .
Há momentos em que um programa está em execução e espera que o número decimal 5 seja inserido no computador. Nesta situação, se a tecla “5” do teclado ideal for pressionada, ainda assim o código de oito bits 00110101 é levado ao microprocessador. Como o que é necessário é o número decimal 5, e não o caractere “5”, um trecho de código (programa curto) da memória usa o microprocessador para converter o código do caractere 00110101 na base dois para o número em complemento de dois 00000101 2 antes de enviá-lo para um local de memória como um byte de complemento de dois. O programador de computador deve ter em mente que 00000101 significa 5 10 na base 2 e é diferente dos números de código 00110101 2 , 35 16 e 53 10 o que significa o caractere “5”. Para exibir o número de complemento de dois 00000101 na memória, outro programa curto precisa converter 00000101 da memória em 00110101. É 00110101, que é igual a 35. 16 que é o mesmo que 53 10 que é exibido no monitor (ou impresso em papel pela impressora).
3.9 Formato de número de ponto flutuante
Um número sem parte decimal é um número inteiro. O número 36 é um número inteiro. 36,375 não é um número inteiro. É um número decimal com uma parte decimal. A parte decimal de 0,375 é uma fração menor que 1.
36.375 é interpretado na forma decimal como:
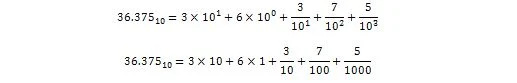
Agora:
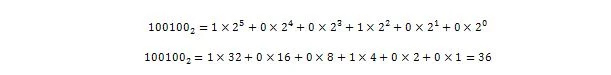
Então, 100100 2 = 3610 que é a parte inteira de 36,375 10 .
Agora:
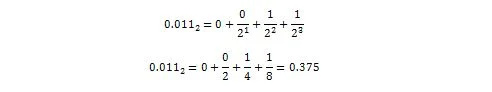
Então, 0,011 2 = 0,375 10 que é a parte decimal de 36,375 10 .
∴ 36.375 10 = 100100,011 2
Dito de outra forma:
100100.011 2 = 36.375 10
Os números são representados no computador na base 2 e não na base 10, sendo tudo igual. Como uma célula em um registro no microprocessador ou uma célula na memória só pode conter 1 ou 0, não há espaço para armazenar um ponto decimal. Isto representa um problema. Como resolução, existe a representação de ponto flutuante de 32 bits de precisão única IEEE-754 e a representação de ponto flutuante de 64 bits de precisão dupla IEEE-754.
Formato de número de ponto flutuante de 32 bits
O número 100100.0112 pode ser expresso como:
100100.011 2 = 1,00100011 2 x 2 +5
O lado direito do símbolo = é referido em matemática como a forma padrão de base dois do lado esquerdo de 100100,011 2 .
Agora, 00100011 de 1,00100011 2 no lado direito do símbolo =, sem o “1” anterior. e sem o 2 como base, é chamado de significando explícito. Neste caso, o ponto binário é levado cinco casas à esquerda para obter o “1”. Não confunda entre ponto decimal e ponto binário. O ponto binário é para a base 2, enquanto o ponto decimal é para a base 10. O “1”. seguido por 00100011 no lado direito do símbolo =, sem o 2 para a base, forma o verdadeiro significado. No entanto, 1,00100011 é chamado de significando implícito.
Depois do significando do lado direito está o “x 2 +5 ”expressão. Com esta expressão, o +5 é chamado de expoente. O sinal de mais significa que o ponto binário deve ser movido cinco casas para frente para estar em sua posição original normal e 2 é a base para a numeração. A equação anterior pode ser escrita ao contrário como:
1.00100011 2 x 2 +5 = 100100,011 2
Com a representação de ponto flutuante de 32 bits, é “1.00100011 2 x 2 +5 ” que é usado e não apenas “100100.011 2 ”. O 2 da base não é registrado. A representação de ponto flutuante de 32 bits para “1.00100011 2 x 2 +5 ”Número, que é igual a 36.375 10 = 100100,011 2 , é mostrado na tabela a seguir:

Existem posições de 32 bits que são numeradas da extremidade direita, começando em 0. O primeiro bit na extremidade esquerda é o bit de sinal. Se o número for positivo, esse bit será 0. Se o número for negativo, esse bit será 1 (-1 consiste em dois caracteres e não pode ser colocado em nenhuma célula). O 1.00100011 2 x 2 +5 que é igual a 36,375 10 que também é igual a 100100,011 2 é um número positivo. Então, o primeiro bit é 0.
Existem oito posições de bits para o expoente, começando da posição 30 até a posição 23, inclusive. Porém, o expoente que está escrito ali é 10000100 2 que é igual a 132 10 . O expoente do número de interesse é na verdade +5 da base de dois. Então, o que acontece?
Agora, no formato de 32 bits, um expoente de 0 é escrito como 01111111 2 que é igual a 127 10 . O +5 10 é +101 2 . Então, ao chegar em 10000100 2 na parte do expoente na tabela, 101 2 foi adicionado a 01111111 2 , correspondentemente. Isso significa que 5 foi adicionado a 127 para obter 132 10 .
O significando, sem “1.”, desceu as posições 22 para 15, inclusive. Observe que o 1 de “1”. não foi indicado na string de 32 bits. Nunca é indicado – aceite isso. O restante das células até a posição 0 são preenchidas com zeros.
Se o expoente real for -5, então 5 será subtraído de 127 10 ter 122 10 . Isso corresponde a subtrair 101 2 de 01111111 2 ter 01111010 2 .
Com toda a ilustração anterior, o número +1 que é igual a 1,0 x 2 0 = 1,0 x 1 = 1,0 é representado como:

Observe que o “1.” de 1,0 x 2 0 não é indicado no formato. Nunca é indicado. A próxima fração mista que vai positivamente depois de 1,0 é:

Observe o 1 na extremidade direita. Esta representação é o número:

A diferença entre 1,0000001192092896 e 1,0 é:
1,0000001192092896 – 1,0 = 0,0000001192092896
Os números com partes decimais são frações mistas. Nem todas as frações entre 1 10 e 2 10 pode ser representado no computador. Pode-se assumir que o menor intervalo fracionário entre os números mistos consecutivos com o formato de ponto flutuante de 32 bits é 0,0000001192092896. Espere que o intervalo para precisão dupla seja menor. Consulte a ilustração a seguir.
Representando o número, 0,0 não segue os argumentos anteriores. A representação para 0,0 é declarada e deve ser aprendida como tal. Para representar 0,0, todas as células do significando são 0 e todas as células do expoente também são zero. O bit de sinal pode ser 0 ou 1. Infelizmente, isso dá origem a 0 positivo e 0 negativo da seguinte forma:

Na vida real, existe apenas um zero. 0 positivo e 0 negativo não existem. No entanto, 0 é geralmente considerado positivo. 0 positivo e 0 negativo existem aqui devido a esta descrição de formato específica. A reta numérica (veja acima) também pode ter +0 e -0, mas existe apenas um zero.
Formato de número de ponto flutuante de 64 bits
O formato de ponto flutuante de 64 bits é semelhante ao formato de 32 bits, mas com as seguintes diferenças:
- Existem 64 bits para representar um número.
- Após o bit de sinal, existem 11 bits para o número do expoente.
- O número do expoente para o índice zero (2 0 ) é 1023 10 = 01111111111 2 .
- Os onze bits são seguidos por 52 bits para o significado explícito.
- Possui uma gama mais ampla de números do que o formato de 32 bits.
Observe que o “1”. que está no início do significando ainda não está incluído entre os 64 bits, assim como não está incluído entre os 32 bits para o formato de 32 bits.
Uma das diferenças mais importantes entre o formato de 64 bits e o formato de 32 bits é que a diferença entre as frações mistas consecutivas no formato de 64 bits é menor do que no formato de 32 bits.
No formato de 64 bits, o intervalo (gap) entre 1,0 e a próxima fração mista pode ser calculado da seguinte forma:
1,0 é
0 01111111111 0000000000000000000 00000000000 000000000000000000000 2
Isso equivale ao “1.”, que não foi indicado na string, multiplicado por 2 elevado à potência (índice) 0 (com o expoente sendo 1023 10 = 01111111111 2 para 2 0 = 1). A corda é 1,0 x 2 0 .
A próxima fração mista maior que 1,0 é:
0 01111111111 0000000000000000000 00000000000 000000000000000000001 2
Isso é equivalente a “1”. que não está indicado na string, seguido de 51 zeros e depois 1, multiplicado por 2 elevado à potência 0 (com o expoente sendo 1023 10 = 011111111112 2 para 2 0 = 1). Isto é o mesmo que:
+2 0 × (1 + 2− -52 ) ≈ 1,000000000000002
O ≈ significa aproximadamente igual a.
Agora:
1,000000000000002 – 1,0 ≈ 0,000000000000002
O valor do intervalo correspondente para um formato de 32 bits é 0,0000001192092896 ≈ 0,00000012.
0,000000000000002 é muito menor que 0,00000012. Portanto, há muito mais frações mistas entre dois números inteiros consecutivos (por exemplo, 3 e 4) no formato de 64 bits do que entre dois números inteiros consecutivos no formato de 32 bits.
O número de frações mistas entre dois inteiros consecutivos na reta numérica é infinito. Portanto, nenhum formato (por exemplo, 32 bits ou 64 bits) pode fornecer todas as frações mistas entre dois números inteiros consecutivos (números inteiros). Quanto menor for o intervalo (intervalo) entre dois números inteiros consecutivos fornecidos por um formato (por exemplo, 32 bits ou 64 bits), maior será o número de frações mistas entre os números inteiros consecutivos (para a reta numérica).
As razões pelas quais o formato de 64 bits é descrito como de precisão dupla ou superior, em comparação com o formato de 32 bits, são que o intervalo entre duas frações mistas consecutivas limitadas por dois inteiros consecutivos para o formato de 64 bits é menor que o correspondente 32 bits. intervalo de formato de bits. Além disso, há mais frações mistas possíveis entre dois números inteiros limitados para o formato de 64 bits do que para o formato de 32 bits.
Convertendo uma parte decimal (fração) de um número decimal em uma parte binária
O 36,375 é um número decimal com a parte decimal de “0,375”. A parte decimal de “.375” é uma fração entre zero e um. O 0,5 na base dez tem o mesmo valor que 1/2 na base dois. O 0,5 10 que é expresso com a expansão de base dois é:
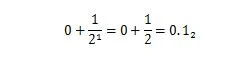
Não é 0,101 2 o que significa 0,625 10 . A parte decimal de um número decimal tem sua parte binária equivalente para o número binário correspondente. Então, para converter um número decimal como 36,375 10 para a base dois, converta 36 em binário e depois converta 0,375 também em binário. Em seguida, junte os dois resultados com o ponto binário. Os métodos para converter as duas seções são diferentes. Como converter um número inteiro decimal para base 2 é explicado no capítulo 1.
Para converter a fração decimal em fração binária, siga as seguintes etapas:
- Multiplique a fração decimal (parte decimal) por 2. O número inteiro resultante é o primeiro dígito binário.
- Repita a etapa anterior com o resultado decimal fracionário para obter o próximo dígito binário.
- Continue repetindo a etapa anterior até que o resultado fracionário decimal seja 0,0000—.
Exemplo: Converta a parte fracionária de 36,375 10 para a parte fracionária equivalente na base dois.
Solução:
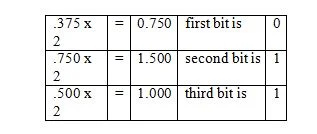
Observe que na terceira etapa, 0,500 foi multiplicado por 2 e não 1,500. A fração binária correspondente é lida na última coluna do topo. E assim, o seguinte resultado é:
0,375 10 = 0,011 2
Convertendo uma parte binária (fração) de um número binário em uma parte decimal
Para conseguir isso, expanda a fração binária em potências recíprocas de 2.
Exemplo: Converta a parte fracionária de 100100,011 2 à parte fracionária equivalente na base dez.
Solução:
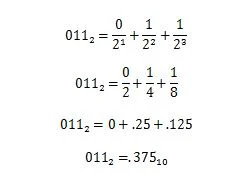
3.10 Prefixos numéricos em computação
Na vida normal, 1 quilo significa 1000, que é abreviado em k (minúsculo) como em 1kg. Na computação, 1 quilo significa 2 10 = 1024, mas é abreviado em K (maiúsculas) como em 1Kbits. Na vida normal, 1 mega significa 1.000.000, que é abreviado em M (maiúsculo) como em 1Mg. Na computação, 1 mega significa 2 vinte = 1.048.576 = 2 10 x 2 10 = 1024 x 1024 = 1.048.576 e ainda é abreviado em M (maiúsculas) como em 1Mbits. Na vida normal, 1 giga significa 1.000.000.000 é abreviado em G (maiúsculo) como em 1Gg. Na computação, 1 giga significa 2 30 = 1.073.741.824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1.073.741.824 e ainda é abreviado em G (maiúsculo) como em 1Gbits. A tabela a seguir dá o significado de quatro prefixos na vida normal e na computação:
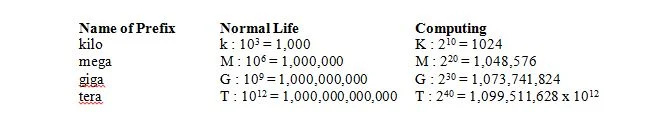
3.11 Problemas
O leitor é aconselhado a resolver todos os problemas de um capítulo antes de passar para o próximo capítulo.
- Desenhe uma reta numérica com números inteiros de -10 a +10.
- Adicione os seguintes números binários em complemento de dois de 8 bits: 101010 2 e 1111 2 .
- Use apenas a abordagem do complemento de dois em 8 bits para subtrair o número binário de 1111 2 do número binário de 101010 2 .
- Encontre o produto de 10110 2 1101 2 na base dois.
- Divida 36.375 10 por 1000 10 em decimal e em binário e compare os resultados.
- Use os 8 bits de sua escolha para ilustrar os lógicos AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right e Rotate Left. Cada byte deve ter uma mistura de 1’s e 0’s.
- a) Escreva o código numérico para o caractere ASCII zero em hexadecimal, binário e decimal.
b) Escreva o código numérico para o caractere ASCII “1” em hexadecimal, binário e decimal.
c) Escreva o código numérico para o caractere ASCII de “A” em hexadecimal, binário e decimal.
d) Escreva o código numérico para o caractere ASCII de “a” em hexadecimal, binário e decimal. - Converter 49,49 10 na base dois. Converta seu resultado no formato de ponto flutuante IEEE de 32 bits.
- a) Qual a diferença entre o formato de ponto flutuante IEEE de 64 bits e o formato de 32 bits?
b) Dê as duas razões relacionadas pelas quais o formato de 64 bits é descrito como tendo precisão dupla ou superior em relação ao
Formato de 32 bits.