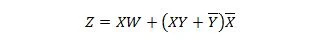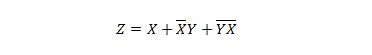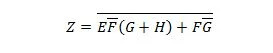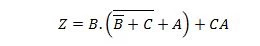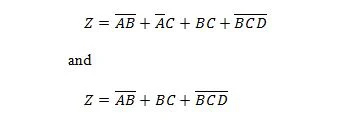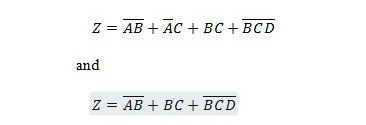Capítulo 2: Álgebra Booleana e seus componentes de computador relacionados
2.1 Operadores Booleanos Básicos
Suponha que eu (o autor) sou alto e você (o leitor) é alto. Se alguém lhe perguntar se nós dois somos altos, você dirá “Sim” (verdadeiro). Se ele perguntar se nós dois somos baixos, você diria “Não” (falso). Se você é baixo e eu alto, e ele pergunta se você ou eu somos altos, sua resposta seria “Sim” (verdadeiro). Se ele perguntar se você e eu somos altos, você não terá uma resposta. Você pode continuar dizendo que a última pergunta não deve ser feita ou que a pergunta não tem resposta. Pois bem, quero que você (leitor) saiba que hoje, em determinadas circunstâncias, a pergunta deve ser feita.
Em biologia, uma pessoa é alta ou baixa. São as condições “ambientais” que fazem com que a pessoa tenha estatura mediana. Um cientista, George Boole, definiu um conjunto de respostas ou regras para este tipo de perguntas. Aprenderemos essas regras nesta seção do curso de carreira online (capítulo). Essas regras são usadas hoje em computação, programação, eletrônica e telecomunicações. Na verdade, sem essas regras você não teria um computador, como é comum hoje; você também não teria programação, como é comum hoje.
Verdadeiro ou falso
Uma simples afirmação em linguagem humana é verdadeira ou falsa em si mesma. Se eu disser “sou alto”, isso é verdadeiro ou falso. Se eu disser “você é alto”, isso é verdadeiro ou falso. Se eu sou alto e você é baixo, e a pergunta é feita se você e eu somos altos, na Lógica Booleana, uma resposta verdadeira ou falsa deve ser dada. Qual destes dois deve ser dado? Boole realmente não respondeu a esta pergunta. Ele simplesmente criou um conjunto de regras para seguirmos. A boa notícia é que, quando você segue essas regras no contexto correto, você não tem nenhuma ambigüidade. Graças a essas regras, hoje temos computadores e programação. As regras são dadas a você agora. As regras não podem realmente ser explicadas; você apenas os aceita. As regras estão sob três títulos: AND, OR e NOT.
E
A pergunta pode ser feita se você E eu somos altos. Minha altura e sua altura são então combinadas pelo conjunto de regras AND. Estas são as regras AND a seguir:
falso E falso = falso
falso E verdadeiro = falso
verdadeiro E falso = falso
verdadeiro E verdadeiro = verdadeiro
Agora, deixe alto ser verdadeiro e curto ser falso. Isso significa que se eu sou baixo E você é baixo, você e eu somos baixos. Se eu sou baixo E você é alto, você e eu somos baixos; essa é a resposta booleana que você deve aceitar. Se eu sou alto E você é baixo, você e eu somos baixos. Se eu sou alto E você é alto, você e eu somos altos. Todas essas são regras AND booleanas que você (o leitor) apenas precisa aceitar.
OU
A pergunta pode ser feita se você OU eu somos altos. Minha altura e sua altura são então combinadas pelo conjunto de regras OR. Estas são as regras OR a seguir:
falso OU falso = falso
falso OU verdadeiro = verdadeiro
verdadeiro OU falso = verdadeiro
verdadeiro OU verdadeiro = verdadeiro
Novamente, deixe alto ser verdadeiro e curto ser falso. Isso significa que se eu sou baixo OU você é baixo, você OU eu é baixo. Se eu sou baixo OU você é alto, você ou eu somos altos. Se eu sou alto OU você é baixo, você OU eu é alto. Se eu sou alto OU você é alto, você ou eu somos altos. Todas essas são regras booleanas que você deve aceitar.
NÃO
Agora, na lógica booleana, existem apenas dois estados (respostas possíveis). Ou seja, se você NÃO é alto, você é baixo. Se você NÃO é baixo, você é alto; nada mais. Estas são as regras NÃO a seguir:
NÃO falso = verdadeiro
NÃO verdadeiro = falso
Suponha que você tenha uma corda (ou mola) que possa estender (puxar). Enquanto a string estiver em seu estado natural, se eu disser “NÃO curta”, você a estenderia; essa é a interpretação. Embora a corda esteja estendida, se eu disser “NÃO longa”, você permitiria que ela se contraísse; essa é a interpretação.
Você tem que memorizar todas as regras fornecidas em suas diferentes categorias.
Mais de dois operandos
Em uma linguagem de computador, AND, OR e NOT são chamados de operadores. Para o operador NOT, você só precisa de um operando (valor para um operador) para ter uma resposta. Para os operadores AND ou OR, você pode ter mais de dois operandos. Os casos anteriores mostram dois operandos para AND e OR. Você pode ter três operandos para AND da seguinte forma:
falso E falso E falso = falso
falso E falso E verdadeiro = falso
Estas são duas linhas; cada um tem dois operadores AND. Na verdade, existem nove linhas quando os operandos são três. Com o operador AND, apenas a última linha (nona linha) é igual a verdadeiro; todas as linhas anteriores são falsas. Observe que com dois operandos para AND, apenas a última linha ainda é verdadeira; todas as três linhas anteriores são falsas. Quando os operandos são quatro, existem 16 linhas e apenas a última linha é verdadeira para o operador AND.
O padrão para AND e o padrão para OR são diferentes. Com três operandos para dois operadores OR, também existem nove linhas e apenas a primeira linha, desta vez, é falsa. A segunda à nona linha é verdadeira. Observe que com dois operandos para OR, apenas a primeira linha ainda é verdadeira; todas as três linhas restantes são falsas. Quando os operandos são quatro para OR, também existem 16 linhas.
O operador NOT lida com apenas um operando. O NOT falso é verdadeiro e o NOT verdadeiro é falso.
2.2 Tabela verdade de dois operandos e seus componentes eletrônicos
Em matemática, existe um tópico chamado álgebra. Uma pequena parte disso foi vista no capítulo anterior. Existe um tipo de álgebra chamada álgebra booleana. Na álgebra booleana, verdadeiro é identificado pelo dígito da base dois, que é 1, e falso é identificado pelo dígito da base dois, que é 0.
Os componentes internos da unidade do computador são componentes eletrônicos. A unidade de sistema do sistema de computador possui componentes eletrônicos digitais. A operação AND é feita por um pequeno componente eletrônico chamado porta AND. A operação OR é feita por um pequeno componente eletrônico chamado porta OR. A operação NOT é feita por um pequeno componente eletrônico chamado porta NOT. Muitas dessas portas podem estar em um chip de circuito integrado (IC).
E Tabela da Verdade e seu Portão
A tabela a seguir fornece a tabela verdade AND e seu símbolo de porta AND (circuito pequeno):
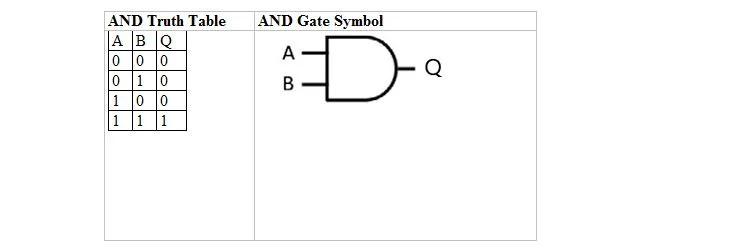
Tanto para a tabela verdade AND quanto para sua porta, A e B são duas variáveis de entrada. Q é a variável de saída. A é 1 ou 0. B é 1 ou 0. Q é 1 ou 0. A tabela verdade AND com 1 e 0 é igual ao layout de verdade AND verdadeiro/falso anterior (tabela). A equação E é:
A . B=Q
onde o ponto (.) significa AND (Booleano). O ponto pode ser omitido para ter AB = Q que significa a mesma coisa (AND).
Nota: Os bits para A e B nas quatro linhas, como pares, são os primeiros quatro números na base dois, começando em 0 (ou 00), ou seja, 00, 01, 10, 11.
A tabela a seguir fornece a tabela verdade OR e seu símbolo de porta OR (circuito pequeno):
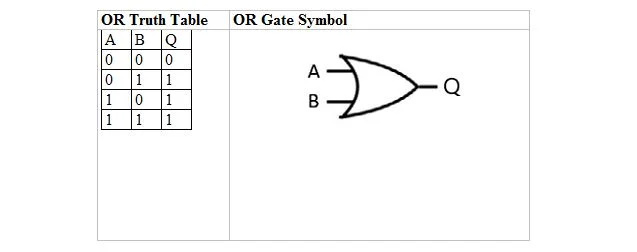
Tanto para a tabela verdade OR quanto para sua porta, A e B são duas variáveis de entrada. Q é a variável de saída. A tabela verdade OR com 1 e 0 é igual ao layout de verdade OR verdadeiro/falso anterior (tabela).
A equação OR é:
A + B = Q
Onde + aqui significa OR booleano e não adição. A equação é lida como “A ou B igual a Q”.
A tabela a seguir fornece a tabela verdade NOT e seu símbolo de porta NOT (circuito pequeno):
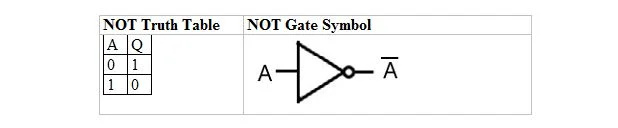
A tabela verdade NOT ou porta NOT possui apenas uma entrada e uma saída. Quando a entrada é 0, a saída é 1. Quando a entrada é 1, a saída é 0. A porta NOT faz uma espécie de inversão. A variável de saída é igual à variável de entrada, mas com uma barra (sobrelinhada). A tabela verdade NOT com 1 e 0 é igual ao layout anterior verdadeiro/falso OR verdade (tabela).
A equação NÃO é:
UMA = Q
Onde Q = A e a barra sobre A aqui significa complemento. O complemento de 0 é 1 e o complemento de 1 é 0. A porta NOT também é conhecida como porta INVERSOR.
Estas são as tabelas verdade fundamentais (ou raiz) e suas portas (pequenos circuitos) na eletrônica digital (com álgebra booleana). As outras três tabelas verdade fornecidas na ilustração a seguir e suas portas são por conveniência e baseiam-se nas três tabelas verdade anteriores.
Existe uma tabela verdade e uma porta que são derivadas da tabela verdade e da porta AND. Eles são chamados de tabela verdade NAND (para NOT AND) e porta NAND correspondente. A tabela verdade NAND e sua porta NAND são:
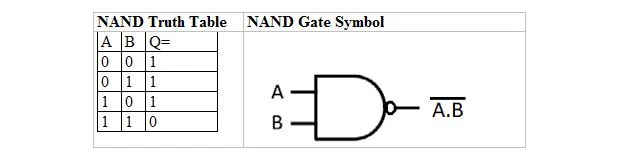
Para obter a tabela verdade NAND, vá até a saída da tabela verdade AND e substitua cada dígito pelo seu complemento. O complemento de 0 é 1 e o complemento de 1 é 0. A porta NAND é como a porta AND, mas possui um pequeno círculo antes da linha de saída. A equação NAND é:
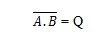
Onde significa o complemento do resultado de “A” E “B”. A barra (over-line) é representada no portão pelo pequeno círculo. Observe que o ponto entre A e B pode ser omitido.
Há outra tabela verdade e porta que são derivadas da tabela verdade e porta OR. Eles são chamados de tabela verdade NOR (para NOT OR) e a porta NOR correspondente. A tabela verdade NOR e sua porta NOR são:
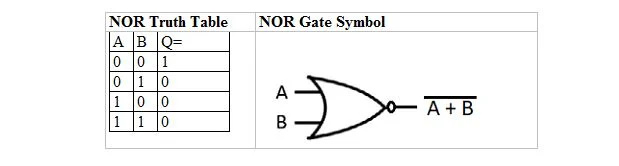
Para obter a tabela verdade NOR, vá até a saída da tabela verdade OR e substitua cada dígito pelo seu complemento. O complemento de 0 é 1 e o complemento de 1 é 0. A porta NOR é como a porta OR, mas possui um pequeno círculo antes da linha de saída. A equação NOR é:
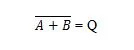
Onde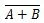 
significa o complemento do resultado de “A” OU “B”. A barra (overline) é representada no portão pelo pequeno círculo.
OU Exclusivo (XOR)
A tabela verdade da porta OR é:
No inglês normal, não está claro se a última linha de 1 OR 1 deve dar 1 ou 0. Portanto, na álgebra booleana, existem dois tipos de tabelas verdade OR e duas portas correspondentes. Com o OR normal, a última linha de 1 OR 1 dá 1. O outro tipo de OR é o OR exclusivo (XOR), onde as três primeiras linhas são iguais às três primeiras linhas do OR normal (incluindo a saída). No entanto, para a quarta e última linha, 1 OR 1 dá 0.
A tabela a seguir fornece a tabela verdade XOR e seu símbolo de porta XOR (circuito pequeno):
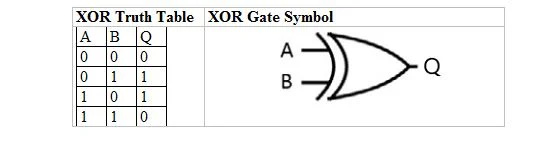
Tanto para a tabela verdade XOR quanto para sua porta, “A” e “B” são duas variáveis de entrada. “Q” é a variável de saída.
A equação XOR é:
A ⊕ B = Q
Onde ⊕ aqui significa XOR booleano.
O OR normal significa um ou ambos. OU exclusivo significa estritamente qualquer e não ambos.
2.3 Postulados Booleanos
Postulados são suposições com base nas quais certas conclusões são tiradas. Existem dez postulados booleanos baseados nas equações AND, OR e NOT (tabelas verdade). Essas equações também são chamadas de funções. As funções fundamentais são recopiadas da seguinte forma:
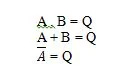
Estas são as funções fundamentais (equações) na álgebra booleana. As outras três equações (funções) a seguir não são funções fundamentais:
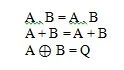
Embora a última função aqui seja peculiar, ela não é considerada uma função fundamental.
Os postulados booleanos são os seguintes:
Da função AND
1) 0 . 0 = 0
vinte . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Da função OR
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Da função NOT
9) 0 = 1
10) 1 = 0
Observação: Esses postulados são apenas as linhas nas tabelas verdade AND, OR e NOT que são expressas de maneira independente. O leitor deve memorizar os postulados dados.
2.4 Propriedades Booleanas
Uma propriedade é uma característica semelhante a algo. Propriedades booleanas são equações derivadas dos postulados booleanos. Nesta seção, as propriedades são simplesmente fornecidas sem suas derivações e usadas posteriormente. Existem vinte e cinco propriedades agrupadas em dez títulos da seguinte forma:
Propriedades da função AND
Propriedade 1:
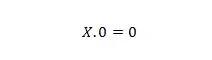
Onde X pode ser 1 ou 0. Isso significa que não importa qual seja X, o resultado é sempre 0.
Nota: Uma variável não deve ser necessariamente A ou B ou C ou D. Uma variável pode ser W ou X ou Y ou Z ou qualquer outra letra.
Propriedade 2:
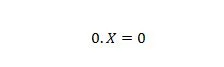
Onde X pode ser 1 ou 0. Observe que a diferença entre a propriedade 1 e a propriedade 2 é que no lado esquerdo do sinal de igual de ambas as equações, as posições de X e 0 são trocadas.
Propriedade 3:
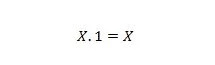
Se X for 0, então 0. 1 = 0. Se X for 1, então 1. 1 = 1.
Propriedade 4:
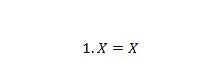
Se X for 0, então 1. 0 = 0. Se X for 1, então 1. 1 = 1. Observe que a diferença entre a propriedade 3 e a propriedade 4 é que no lado esquerdo de ambas as equações, as posições de X e 1 são trocados.
Propriedades da função OR
Propriedade 5:
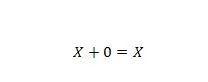
Onde X pode ser 1 ou 0. Isso significa que se X for 0, o resultado será 0. Se X for 1, o resultado será 1.
Propriedade 6:
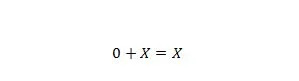
Onde X pode ser 1 ou 0. Observe que a diferença entre a propriedade 5 e a propriedade 6 é que no lado esquerdo de ambas as equações, as posições de X e 0 são trocadas.
Propriedade 7:
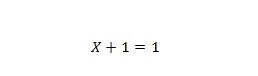
Se X for 0, então 0 + 1 = 1. Se X for 1, então 1 + 1 = 1.
Propriedade 8:
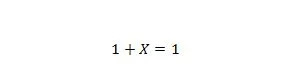
Se X for 0, então 1 + 0 = 1. Se X for 1, então 1 + 1 = 1. Observe que a diferença entre a propriedade 7 e a propriedade 8 é que no lado esquerdo de ambas as equações, as posições de X e 1 são trocados.
Propriedades relativas à combinação de uma variável consigo mesma ou com seu complemento
Propriedade 9: 
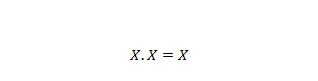
Ou seja: se X for 0, então 0 . 0 = 0. Se X for 1, então 1. 1 = 1.
Propriedade 10:
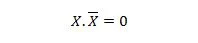
Ou seja: se X for 0, então 0,1 = 0. Se X for 1, então 1,0 = 0.
Para variáveis consecutivas, esta propriedade torna-se:
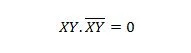
Propriedade 11:
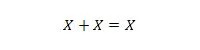
Ou seja: se X for 0, então 0 + 0 = 0. Se X for 1, então 1 + 1 = 1 (do OR normal).
Propriedade 12:
Ou seja: se X for 0, então 0 + 1 = 1. Se X = 1, então 1 + 0 = 1.
Ou seja: se X for 0, então 0 + 1 = 1. Se X = 1, então 1 + 0 = 1.
Dupla Complementação
Propriedade 13:
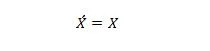
Quando X no lado esquerdo é 0, X no lado direito torna-se 0. Quando X no lado direito é 1, X no lado esquerdo torna-se 1. Em outras palavras, complementos duplos devolvem o valor original.
Lei comutativa
Propriedade 14:
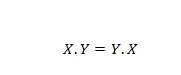
Isso significa que a troca do primeiro e do segundo operandos do operador AND, no lado esquerdo do sinal de igual, não importa; a resposta ainda é a mesma após a troca do lado esquerdo ter ocorrido. Esta equação pode ser escrita com os pontos omitidos como: XY = YX.
Propriedade 15:
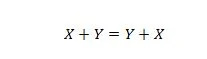
A explicação aqui é a mesma do AND anterior, mas é para o operador OR.
Direito Distributivo
Propriedade 16:
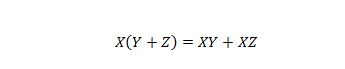
Aqui existem três variáveis: X, Y e Z. Cada variável pode ser 1 ou 0. No lado esquerdo do símbolo de igual, os colchetes significam avaliar primeiro o que há neles. Então, AND é o resultado com X. O lado direito diz que X E Y juntos, OU X E Z juntos, são iguais ao lado esquerdo. Observe que o operador ponto para os ANDs é totalmente omitido; e as variáveis unidas ainda significam AND.
Propriedade 17:
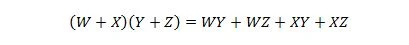
Esta propriedade é uma extensão da propriedade 16 com a variável adicionada W.
Direito Associativo
Propriedade 18:
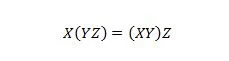
Colchetes significam avaliar primeiro o que está entre colchetes. Portanto, para a expressão do lado esquerdo, se Y com Z são ANDed primeiro, e X é ANDed com o resultado, então o resultado final do lado esquerdo é igual ao resultado final do lado direito - lado da mão onde X com Y recebe AND primeiro antes de AND do resultado com Z. Observe que os pontos foram omitidos na equação.
Propriedade 19:
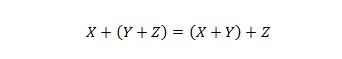
Esta propriedade é explicada de forma semelhante à propriedade 18, mas o operador OR é empregado em vez do operador AND. O operador OR + nunca é omitido de uma expressão booleana por questão de simplicidade. Por outro lado, o operador AND pode ser omitido e as duas variáveis podem ser unidas.
Absorção
Propriedade 20:
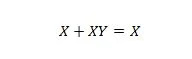
Com esta equação, não importa qual seja Y, o lado direito sempre será X (absorvido).
Propriedade 21:
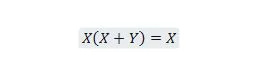
Além disso, com esta equação, não importa qual seja Y, o lado direito sempre será X (absorvido). Esta propriedade 21 é igual à propriedade 20, que é:
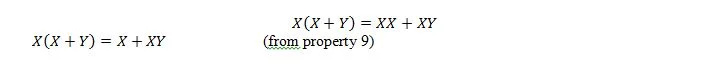
Aqui, usamos a lei distributiva e o fato de que X.X = X da propriedade 9.
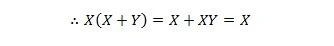
Uma identidade
Propriedade 22:
Isso significa que para a expressão X + Y, o complemento de X na frente de Y não altera a expressão.
Propriedade 23:
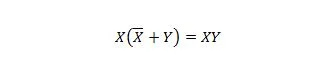
Isso significa que para a expressão XY, o complemento de X ORed com Y entre colchetes, que é feito primeiro, não altera a expressão XY.
Lei de DeMorgan
Propriedade 24:
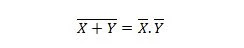
Isso significa que uma porta NOR (NOT OR) tem o mesmo resultado que notar as duas entradas antes de fazer AND delas.
Propriedade 25:
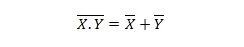
Isso significa que uma porta NAND (NOT AND) tem o mesmo resultado que notar as duas entradas antes do OR.
As ilustrações fornecidas são as 25 propriedades. Eles podem ser comprovados substituindo todos os diferentes valores possíveis de 1 e 0, em cada expressão do lado esquerdo, para ver se a expressão (ou resultado) do lado direito é obtida. As provas ficam como exercício para o leitor.
2.5 Simplificação de Expressões Compostas
As duas funções a seguir são iguais:
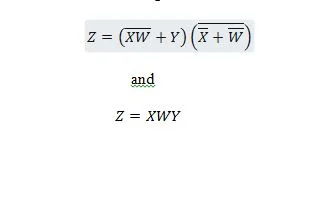
Z é a saída e X, W e Y são as entradas. O primeiro precisa de uma porta NAND, uma porta OR, uma porta AND, duas portas NOT, uma porta OR e uma porta NOR. O segundo precisa de apenas duas portas AND. A primeira é uma equação com uma expressão composta, do lado direito, que foi simplificada (reduzida) ao único termo de expressão do lado direito para a segunda equação.
A simplificação ou redução leva a um menor número de portas para implementar a mesma função de um circuito. Esse circuito menor pode fazer parte de um circuito integrado (IC) ou ser um circuito independente na superfície da placa-mãe do computador.
Quando uma função (equação) chega ao processo de projeto, é necessário simplificar para reduzir o número de portas e acabar com um circuito mais barato. A simplificação necessita do emprego de uma ou mais das vinte e cinco propriedades booleanas anteriores.
Exemplo 2.51:
Reduza a equação:
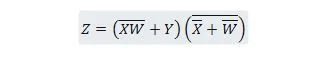
Observação: Dois parênteses próximos um do outro significa que os parênteses são AND (o ponto entre eles opcionalmente não foi escrito).
Solução:
Para as soluções, a justificativa (motivo) de cada passo é dada à direita do passo, entre parênteses. O leitor deverá ler cada etapa e sua justificativa. O leitor também deve consultar as propriedades anteriores ao ler as etapas de redução da função.
Exemplo 2.52:
Simplificar:
2.6 Soma Mínima de Produtos
As duas funções a seguir são iguais:
Diz-se que ambas as expressões à direita de ambas as equações estão na forma de Soma de Produtos (SP). Diz-se que uma expressão expressa está na forma Soma do Produto se não tiver parênteses. É óbvio que a primeira função (equação) precisa de mais portas do que a segunda função.
A primeira expressão à direita ainda pode ser reduzida para obter a segunda função. A segunda expressão do lado direito não pode ser mais simplificada e ainda assim ser expressa como Soma de Produtos (“adição” de termos). A segunda expressão do lado direito não pode ser mais simplificada. Portanto, diz-se que está na forma Soma Mínima de Produtos (MSP).
Exemplo 2.61:
Traga a seguinte função primeiro para o formulário Soma de Produtos e depois para o formulário Soma Mínima de Produtos.
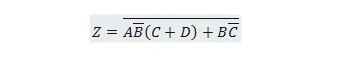
Solução:
Ao resolver problemas como este, uma ou mais das vinte e cinco propriedades anteriores devem ser usadas conforme ilustrado nesta solução:
2.6 Soma Mínima de Produtos
As duas funções a seguir são iguais:
Diz-se que ambas as expressões à direita de ambas as equações estão na forma de Soma de Produtos (SP). Diz-se que uma expressão expressa está na forma Soma do Produto se não tiver parênteses. É óbvio que a primeira função (equação) precisa de mais portas do que a segunda função.
A primeira expressão à direita ainda pode ser reduzida para obter a segunda função. A segunda expressão do lado direito não pode ser mais simplificada e ainda assim ser expressa como Soma de Produtos (“adição” de termos). A segunda expressão do lado direito não pode ser mais simplificada. Portanto, diz-se que está na forma Soma Mínima de Produtos (MSP).
Exemplo 2.61:
Traga a seguinte função primeiro para o formulário Soma de Produtos e depois para o formulário Soma Mínima de Produtos.
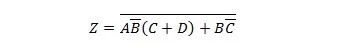
Solução:
Ao resolver problemas como este, uma ou mais das vinte e cinco propriedades anteriores devem ser usadas conforme ilustrado nesta solução:
Esta última expressão está na forma Soma de Produtos (SP), mas não na forma Soma Mínima de Produtos (MSP). A primeira parte da pergunta foi respondida. A solução para a segunda parte é a seguinte:
Esta última função simplificada (equação) está na forma MSP e necessita de menos portas para implementação do que sua forma SP correspondente. Lembre-se: SP significa Soma de Produtos enquanto MSP significa Soma Mínima de Produtos.
Exemplo 2.62:
O circuito a seguir possui as entradas X, Y e W e Z é a saída. Produza a função Soma de Produtos (SP) (função de soma mínima aparente de produtos) para Z. Em seguida, produza a Soma de Produtos (MSP) verdadeira mais reduzida (minimizada). Em seguida, implemente o circuito MSP (desenhe a rede de portas MSP).
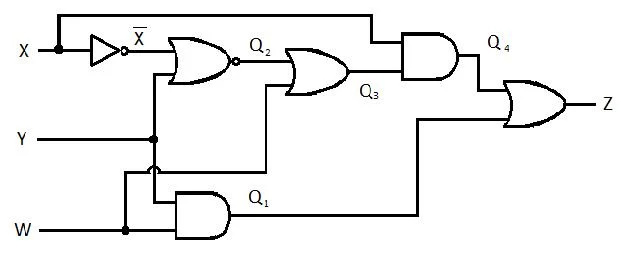
Fig 2.61 Um Circuito de Gating
Solução:
Antes de iniciar o processo de simplificação, a expressão para Z deve ser obtida em termos de X, Y e W. Consulte este exemplo de ilustração do diagrama:
Esta é a expressão de Z em termos de X, Y e W. Depois disso, a simplificação para MSP aparente pode ocorrer. MSP aparente é SP.
Esta última equação (função) está na forma SP. Não é verdade Soma Mínima de Produtos (ainda não é MSP). Portanto, a redução (minimização) tem de continuar.
Esta última equação (função) é uma verdadeira Soma Mínima de Produtos (MSP). E o circuito de ativação da Soma Mínima de Produtos (minimização verdadeira) é:
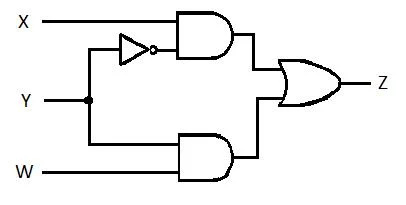
Fig 2.62 Circuito de Gating MSP
Comente
A partir da análise desta seção, pode-se observar que não está claro se a Soma dos Produtos é a Soma Mínima dos Produtos ou não. SP não é muito útil. É o MSP que é muito útil. Existe uma forma segura de obter MSP; é usar o Mapa de Karnaugh. Karnaugh Map está além do escopo deste curso de carreira online.
2.7 Problemas
O leitor é aconselhado a resolver todos os problemas de um capítulo antes de passar para o próximo capítulo.
- Produza as tabelas verdade AND, OR e NOT com suas portas correspondentes.
- Escreva os dez Postulados Booleanos em suas diferentes categorias, nomeando as categorias.
- Sem explicação, escreva as vinte e seis propriedades da álgebra booleana em suas diferentes categorias, nomeando as categorias.
- Reduza a equação usando as propriedades booleanas e citando as categorias utilizadas.
- Reduza a equação usando as propriedades booleanas e citando as categorias utilizadas.
- Usando as propriedades booleanas e citando as categorias utilizadas, reduza a seguinte equação – primeiro para Soma de Produtos e depois para Soma Mínima de Produtos:
- Usando as propriedades booleanas e citando as categorias utilizadas, reduza a seguinte equação – primeiro para Soma de Produtos e depois para Soma Mínima de Produtos:
